Algorithms Problem Solving: Convert Sorted Array to Binary Search Tree

Photo by Milad Fakurian

This post is part of the Algorithms Problem Solving series.

Problem description

This is the Convert Sorted Array to Binary Search Tree problem. The description looks like this:

Given an integer array nums where the elements are sorted in ascending order, convert it to a height-balanced binary search tree.

A height-balanced binary tree is a binary tree in which the depth of the two subtrees of every node never differs by more than one.

Examples

Example 1:

Input: nums = [-10,-3,0,5,9]
Output: [0,-3,9,-10,null,5]

Example 2:

Input: nums = [1,3]
Output: [3,1]

Example 3:

Input: nums = [1,3]
Output: [3,1]

Solution

To construct a height-balanced binary search tree, we can break down the array into the middle, create a new node based on the middle number, go to the left, do the same process, go to the right, and also do the same process.

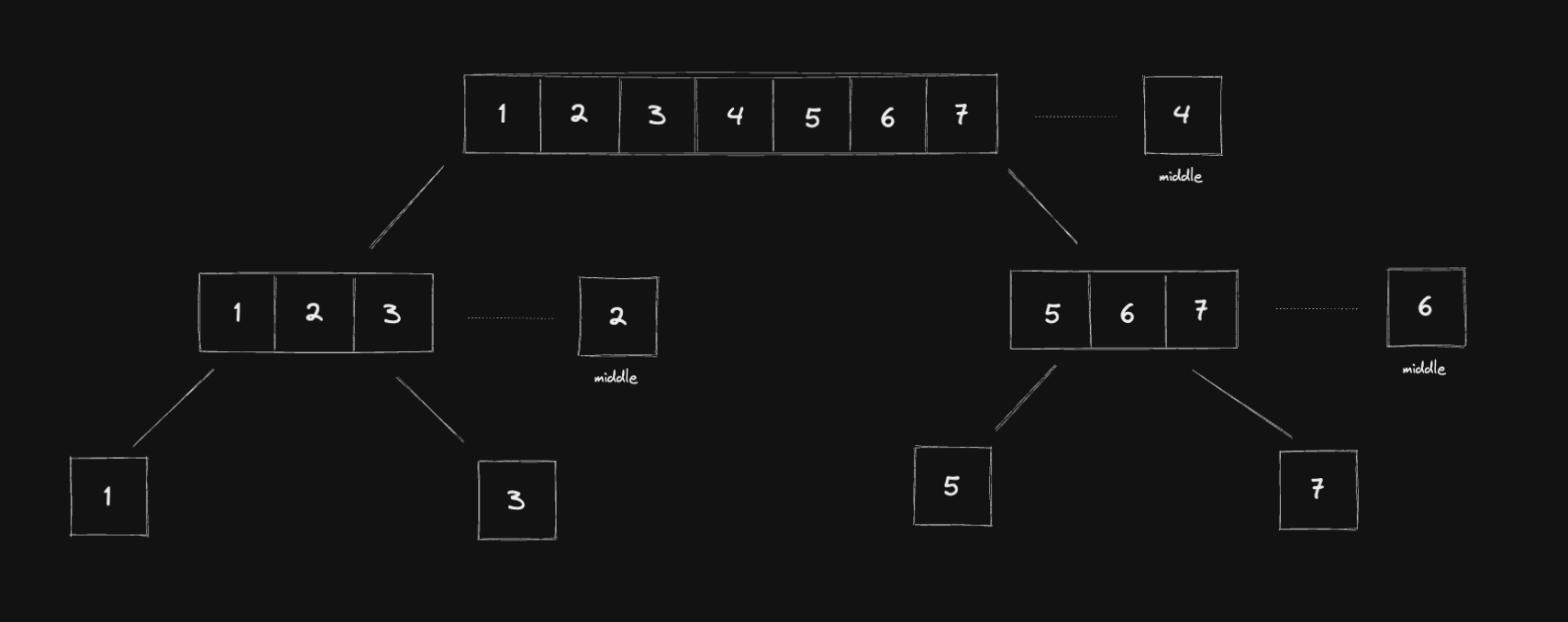
This picture illustrates the process:

1. go to the middle

2. create a new node based on this middle number

3. go to the left

   3.1. cut the array from the start to the middle - 1
   3.2. create a new node based on this middle number
   3.3. go to the right and the left

4. go to the right

   4.1. cut the array from the middle + 1 to the end
   4.2. create a new node based on this middle number
   4.3. go to the right and the left

You can see that the third and forth steps we can implement by recursively call the function. We just need to adjust the data structure.

function sortedArrayToBST(nums) {
  if (nums.length === 0) return null;

  const middle = Math.floor(nums.length / 2);
  const num = nums[middle];
  const node = new TreeNode(num);

  node.left = sortedArrayToBST(nums.slice(0, middle));
  node.right = sortedArrayToBST(nums.slice(middle + 1, nums.length));

  return node;
}

And this is the generated binary search tree with balanced height:

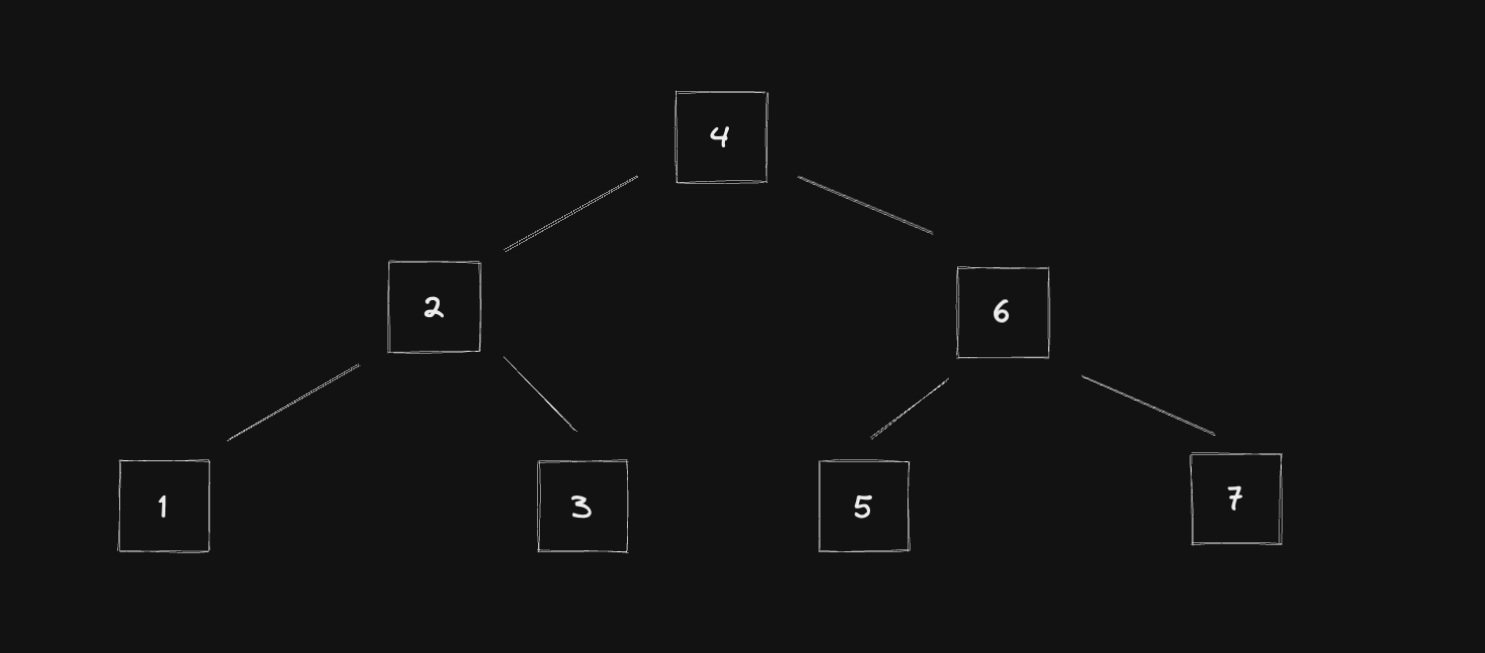
Resources

• Algorithms Problem Solving Series
• Algorithms & Data Structures studies
• Data Structures in JavaScript Series
• Stack Data Structure in JavaScript
• Queue Data Structure in JavaScript
• Linked List Data Structure in JavaScript
• Stack Data Structure
• Queue Data Structure
• Linked List
• Tree Data Structure

Twitter · Github